《Single Digit Patterns(Empty Rectangle)》
上級のテクニックでは 2つ以上の領域(行,列,大マス) の中を検討することによって 排除される数字を見つけます。 このページでは Single Digit Patterns と呼ばれるテクニックの1つである
・カーブミラー排除[Empty Rectangle]
を説明します。
Single Digit Patterns と呼ばれるテクニック は 1つの数字(Single Digit)がある条件を満たすように配置されている(Pattern)時に, その数字を配置できないマスが見つかる というものです。 カーブミラー排除(Empty Rectangle)だけでなく, 賢い見張兵排除(X-Wing)などの Fish系のテクニック, 筋違見張塔排除(Skyscraper, 2-String Kite, Turbot Fish)も Single Digit Patterns に属するテクニックです。
カーブミラー排除(Empty Rectangle)を ある条件(領域で配置可能なマスが2つに限られる)を満たす 1つの領域(行 または 列)に属する2つのマス に注目し, それらのマスを起点として 翼を広げるように それらのマスが属する2つの領域を検討していき, その数字 を排除することができるマスを見つけるテクニックと解釈すれば, カーブミラー排除(Empty Rectangle)は Wing系のテクニック と考えることもできます。
 [Empty Rectangle]
[Empty Rectangle]
 [テクニック]
[テクニック]
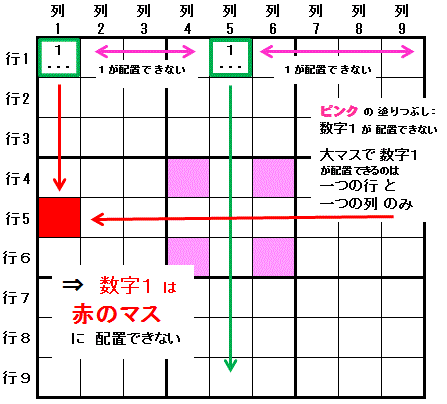
最初に ある数字(数字1)が 配置できるマスが2つ(行1列1,行1列5)に限られる領域(行1)を見つけます。
その2つのマスのうちの一つのマス(行1列5)が属する領域(列5) と それとクロスする一つの領域(行5)にのみ 数字1 が配置可能な 大マス(大マス5)が存在すると, この領域(行5)と,最初に配置可能だった2つのマスのうちのもう一つのマス(行1列1)と同じ領域(列1)にあるマス(行5列1)には, 数字1 を配置できません。
説明) もし,行5列1 に 数字1 が配置されると, 数字1 は 行1列1 に配置できなくなります。 また 数字1 は 大マス5 の 行5 に配置できなくなるので, 大マス5 で 列5 に配置されることになります。 すると 数字1 は 行1列5 に配置できなくなります。 行1 で 数字1 は 行1列1,行1列5 にのみ配置可能だったので, 数字1 が 行1 で配置できるマスがなくなり,矛盾を生じます。
[名称”カーブミラー排除”の由来]
本通り(行1)には 2つの交番(行1列1,行1列5)があり,交通巡査(数字1)は どちらかの交番に詰めています。 一つの交番(行1列5)を通る連絡筋(列5)と裏通り(行5)との交差点(大マス5)にカーブミラーが設置されていると, もう一つの交番(行1列1)を通る連絡筋(列1)と裏通り(行5)との交差点(行5列1)は, 交通巡査がどちらの交番に詰めていても監視可能なので,その交差点(行5列1)に交通巡査(数字1)を配置する必要はありません。
[テクニック”カーブミラー排除”の適応に関する注意]
行 と 列 を入れ替えても カーブミラー排除は成立します。
配置できるマスが2マスに限られる行(列)と大マスで配置可能な行が一つに限られる行(列)が同じ Floor(Tower)にある場合は カーブミラー排除は成立しません。
ある行(列)で配置可能なマスが2つに限られた2マスが同じ Tower(Floor)にある場合は カーブミラー排除は成立しません。
Floor:横に3つ並んだ大マス
Tower:横に3つ並んだ大マス

上級のテクニックでは 2つ以上の領域(行,列,大マス) の中を検討することによって 排除される数字を見つけます。 このページでは Single Digit Patterns と呼ばれるテクニックの1つである
・カーブミラー排除[Empty Rectangle]
を説明します。
Single Digit Patterns と呼ばれるテクニック は 1つの数字(Single Digit)がある条件を満たすように配置されている(Pattern)時に, その数字を配置できないマスが見つかる というものです。 カーブミラー排除(Empty Rectangle)だけでなく, 賢い見張兵排除(X-Wing)などの Fish系のテクニック, 筋違見張塔排除(Skyscraper, 2-String Kite, Turbot Fish)も Single Digit Patterns に属するテクニックです。
カーブミラー排除(Empty Rectangle)を ある条件(領域で配置可能なマスが2つに限られる)を満たす 1つの領域(行 または 列)に属する2つのマス に注目し, それらのマスを起点として 翼を広げるように それらのマスが属する2つの領域を検討していき, その数字 を排除することができるマスを見つけるテクニックと解釈すれば, カーブミラー排除(Empty Rectangle)は Wing系のテクニック と考えることもできます。
 [Empty Rectangle]
[Empty Rectangle]
 [テクニック]
[テクニック]最初に ある数字(数字1)が 配置できるマスが2つ(行1列1,行1列5)に限られる領域(行1)を見つけます。
その2つのマスのうちの一つのマス(行1列5)が属する領域(列5) と それとクロスする一つの領域(行5)にのみ 数字1 が配置可能な 大マス(大マス5)が存在すると, この領域(行5)と,最初に配置可能だった2つのマスのうちのもう一つのマス(行1列1)と同じ領域(列1)にあるマス(行5列1)には, 数字1 を配置できません。
説明) もし,行5列1 に 数字1 が配置されると, 数字1 は 行1列1 に配置できなくなります。 また 数字1 は 大マス5 の 行5 に配置できなくなるので, 大マス5 で 列5 に配置されることになります。 すると 数字1 は 行1列5 に配置できなくなります。 行1 で 数字1 は 行1列1,行1列5 にのみ配置可能だったので, 数字1 が 行1 で配置できるマスがなくなり,矛盾を生じます。
[名称”カーブミラー排除”の由来]
本通り(行1)には 2つの交番(行1列1,行1列5)があり,交通巡査(数字1)は どちらかの交番に詰めています。 一つの交番(行1列5)を通る連絡筋(列5)と裏通り(行5)との交差点(大マス5)にカーブミラーが設置されていると, もう一つの交番(行1列1)を通る連絡筋(列1)と裏通り(行5)との交差点(行5列1)は, 交通巡査がどちらの交番に詰めていても監視可能なので,その交差点(行5列1)に交通巡査(数字1)を配置する必要はありません。
[テクニック”カーブミラー排除”の適応に関する注意]
行 と 列 を入れ替えても カーブミラー排除は成立します。
配置できるマスが2マスに限られる行(列)と大マスで配置可能な行が一つに限られる行(列)が同じ Floor(Tower)にある場合は カーブミラー排除は成立しません。
ある行(列)で配置可能なマスが2つに限られた2マスが同じ Tower(Floor)にある場合は カーブミラー排除は成立しません。
Floor:横に3つ並んだ大マス
Tower:横に3つ並んだ大マス





